Continuous vs Discrete

Gaussian distributions are a type of continuous probability distribution. So before getting into the details about Gaussian distributions, let's review the differences between a continuous and discrete distribution.

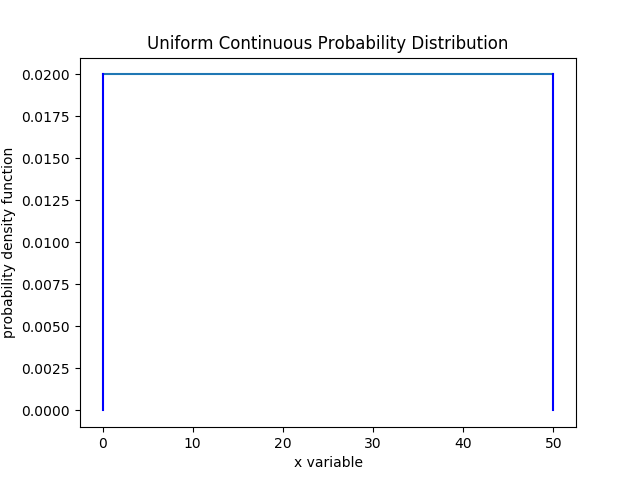
As a reminder, a continuous probability distribution is associated with a continuous variable like height, weight, distance, velocity, angle, etc.

You've been working with a uniform continuous probability distribution like the following example.

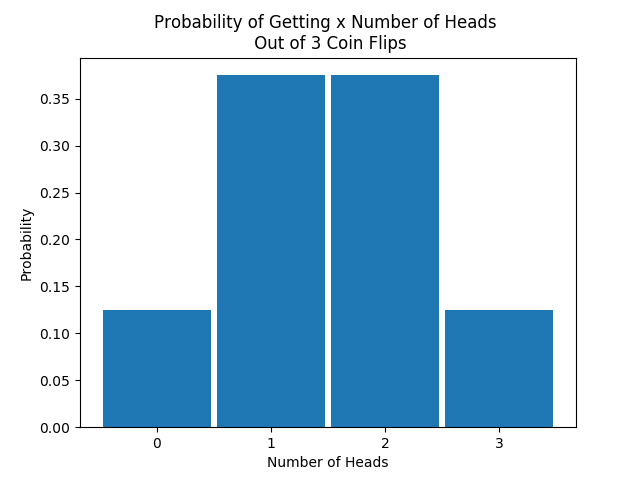
On the other hand, a discrete distribution is associated with variables that can only take on certain values like coin flips, dice rolls or location on a grid. This is an example of a discrete distribution.

Continuous Distributions

The uniform continuous probability distribution is just one of many continuous probability distributions that exist. Take a look at this Wikipedia page, List of Continuous Distributions, just to get a sense for how many there are.

What do all of these distributions have in common? They represent the probability of events occurring for continuous variables. Different applications will use different distributions.

For example, when modeling probabilities of a spinning wheel, you used a uniform distribution. When modeling uncertainty in a sensor measurement, you'll use a Gaussian distribution.

Gaussian Distribution

In order to understand uncertainty in self-driving cars, you should at least have a basic knowledge of the Gaussian distribution. The uncertainty in a sensor measurement or the location of a pedestrian, for example, is oftentimes modeled with a Gaussian distribution.

This next part of the lesson will give a broad overview of the Gaussian distribution and where the distribution comes from.

However, this is not a complete statistics course. This will be a brief overview of this particular distribution and assumes you're familiar with terms like mean, standard deviation, population, and sample where:

• population refers to the entire set of all data points. Like if you were measuring people's weights, then the population would be all people in the world.
• sample refers to a part of the population. In the weights example, you might take a random sample of the population since it would be practically impossible to measure the weights of all humans.
• mean is the average value, which in this case would be the average weight of all humans.
• standard deviation measures the spread in the data. Does the data tend to hover around the mean, or is the data more spread out?

If you aren't familiar with these terms or need a refresher, here is a resource that you might find helpful: sample vs population.